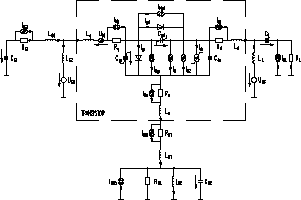
Figure 3: Equivalent circuit of the oscillator to be optimized [1].
A low phase noise is besides the signal properties essential to the design of oscillating electrical circuits. A new and general method to minimize the single-sideband phase noise of free running oscillators reduces the phase noise without requiring additional elements or the manufacture of prototypes. It is based on the description of the signal and noise behavior of an oscillator circuit by the Langevin equations
where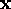 
are the state variables of the circuit,
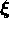are the white noise sources
and y is a nonlinear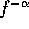 
noise source denoting the baseband
noise.
The notation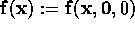 
is used.
The terms of order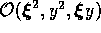 
are neglected.
The single-sideband phase noise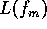 
can be simulated by solving (5)
with a perturbation theory [8]
The first term on the right hand side of Eq. (6) describes
the phase noise
caused by the white noise sources.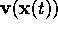 
is the left-sided
eigenvector of the fundamental matrix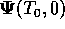 
.
The matrix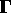 
denotes the correlation
matrix of the white noise sources. The second term
of Eq. (6) describes the phase noise
caused by the baseband noise.
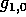is a coefficient that characterizes
the upconversion of the baseband noise to the carrier frequency. The
modulation of the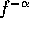 
noise source due to the oscillation is taken
into account as well as the upconversion of the baseband noise caused by
the nonlinearities in the circuit.
The factor c is derived from baseband noise measurements.
The functions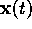 
and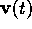 
depend on
the design parameters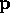 
of the circuit by
the system of nonlinear
differential equations
and appropriate boundary conditions.
The minimization of the phase noise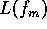 
with respect to the design parameters
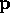and subject to Eqs. (7) and (8)
is an optimal control problem with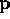 
as control from a finite dimensional control space
and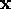 
and 
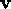as state variables
of the optimal control problem.
The optimization problem is solved numerically by
the direct collocation method [1],
[14].
In an experiment the method is applied to minimize the single-sideband phase noise of a planar integrated free running microwave oscillator at 15 GHz [1]. The equivalent circuit of the oscillator is depicted in Fig. 3. In this special case, five design parameters of the linear network are optimized subject to a system of 20 highly nonlinear differential equations (7), (8). A prototype of the new designed oscillator has been manufactured. A reduction of 10 dB of the phase noise caused by the upconverted baseband noise is measured at a frequence deviation of 10 kHz [1].
