


Next: References
Up: No Title
Previous: P3. Optimum design
Methods for the solution of
optimal control problems are the recently developed
and implemented direct collocation and direct shooting methods
(cf. [3], [6],
[13], [14]).
These methods have shown to be efficient, reliable and robust
in solving real-life problems.
If very high accuraccy is required then
the indirect multiple shooting method is the choice [4].
A survey of efficient methods is given in [11].
Efficient methods for the solution of the mentioned parameter identification
problems are based on multiple shooting in combination
with generalized Gauss-Newton- or adapted SQP-methods (cf. [2], [7]).
These identification algorithms only
require some
functions of the states 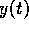 and no derivatives
to be measured in order to
identify the unknown parameters p. In other widely used approaches it
is necessary to measure not only the first but also the
second time derivatives of the state variables
and no derivatives
to be measured in order to
identify the unknown parameters p. In other widely used approaches it
is necessary to measure not only the first but also the
second time derivatives of the state variables 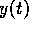 .
As this is often not practicable,
artifical measurements of time derivatives have to be constructed.
.
As this is often not practicable,
artifical measurements of time derivatives have to be constructed.
The proposed methods for identification and optimal control
use the same dynamic model.
They can therefore be conviently used in combination.
Acknowledgement.
This research has been supported in part
by the Deutsche Forschungsgemeinschaft (DFG),
the Bundesministerium für Forschung und Technologie (BMFT)
and the Bayerische Forschungsstiftung
within the
Bayerischer Forschungsverbund für technisch-wissenschaftliches
Hochleistungsrechnen (FORTWIHR).
Oskar von Stryk
Thu May 2 20:47:39 MET DST 1996
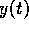 and no derivatives
to be measured in order to
identify the unknown parameters p. In other widely used approaches it
is necessary to measure not only the first but also the
second time derivatives of the state variables
and no derivatives
to be measured in order to
identify the unknown parameters p. In other widely used approaches it
is necessary to measure not only the first but also the
second time derivatives of the state variables 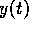 .
As this is often not practicable,
artifical measurements of time derivatives have to be constructed.
.
As this is often not practicable,
artifical measurements of time derivatives have to be constructed.