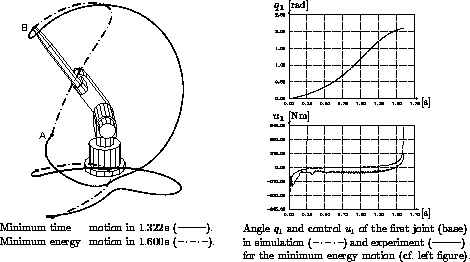
Figure 1: An example of robot trajectory optimization.
The application of numerical optimization methods
to trajectory optimization for industrial robots has shown
that large improvements are possible compared with traditional
path planning methods (e.g., [9], [15]).
But the use of sophisticated numerical optimization methods
requires several necessities as, e.g., the proper
description of the dynamic behavior of the robot as an n-body system
(in minimal coordinates, e.g., the relative angles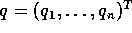 
between successive joints of the robot)
where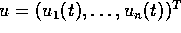 
is the torque control, M is
the positive definite and symmetric (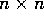
)-matrix
of moments of inertia and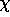 
are
the moments resulting from centrifugal, coriolis, gravitational and frictional
forces.
Thus the first basic problem is the modelling of the dynamic system (1)
of the robot [16].
The identification
of unknown dynamic parameters of the specific robot (as, e.g., moments of inertia
or friction parameters) is a second must (see problem P2).
Once the dynamic equations have been modelled
and determined in a proper way, the optimization of trajectories
can be investigated.
Different tasks for
robots require different objectives for optimal trajectories,
e.g., in welding optimal tracking of the prescribed path might be required.
Otherwise if only the initial and the final position of the robot
are prescribed a fast point-to-point movement might be requested.
It has been demonstrated that the fastest
point-to-point motion (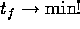
)
exhibits quite often a surprisingly structure,
impacts enormous stress on the links
and can even often not be realized in practice.
Here,
fast minimum energy motions (
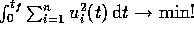) offer a compromise between
time and stress [15].
The robot trajectories also have to satisfy
several constraints as, e.,g.,
constraints on the controls, the angles and the angular velocities.
Further constraints result from the
geometrical design of the robot's working cell
and require an efficient modelling of collision avoidance.
