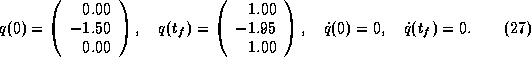
All computations have been performed on a SUN Sparc station 2
with 40 MHz.
A special quarter rotation around the base of the robot
is investigated with a load of 0 kg
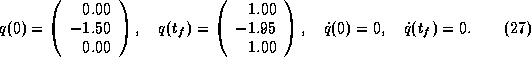
The direct collocation method is at first applied to
the state constrained minimum time problem with
i=1,2,3,
and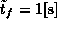 
as initial estimates of the
unknown solution.
A first solution is obtained for 7 equidistant grid points.
A refinement of the discretization yields a sequence
of nonlinear programming problems with increasing dimensions
ending up in an 81 grid point solution.
The convergence history is shown in Table 1
where NGRID is the number of grid points of the direct collocation
method DIRCOL, NY is the number of degrees of freedom of the nonlinear program,
NLEQ is the number of nonlinear equality constraints of the nonlinear program,
NITER is the number of iterations of the SQP-method NPSOL [9],
NZJAC is the percentage of non zero Jacobian elements in the nonlinear program,
CPU-Sec is the computing time in seconds,
NDEQ is the number of differential equations of the multi-point boundary value
problem of the necessary conditions,
NKNOT is the number of multiple shooting nodes used in BNDSCO,
NS is the number of switching points,
NITER is the number of Newton iterations in BNDSCO.
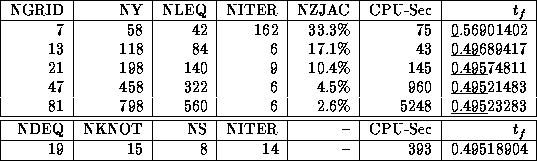
Table 1: Convergence history of the first time optimal motion.
Remark 1. The inequality constraints on state and control variables
are treated as box constraints in the nonlinear program.
Therefore no nonlinear inequality
but only equality constraints appear
in the discretized problem.
Remark 2. To compare the time optimal with the minimum energy solution
a seventh state variable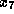 
has been used in the computations.
Therefore the computing time for the time optimal motion
will in fact be less than the reported times
if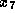 
is not computed in the optimization.
Remark 3. It is a remarkable fact the the number of SQP-iterations
is not increasing with the number of degrees of freedom
in the nonlinear program.
The increase in computing time is due to the fact
that the sparsity patterns in the gradients
are not yet used in the linear algebra of the quadratic
programming subproblems. Much efficiency can still be gained
if an appropriate sparse linear algebra is used
(cf. Betts, Huffman [1] and Gill [8]).
From the solution for 81 grid points the switching structure is guessed, i. e., number and type of the switching points. With this switching structure and the state and the estimated adjoint variables from the direct collocation method the multiple shooting method is successfully applied to solve the multi-point boundary value problem of optimality conditions. The solution of the direct collocation method is shown with the solution of the multiple shooting method in Figure 3, the initial guess and the finally obtained switching points are listed in Table 2, and the qualitative behaviour of the switching structure is shown in Figure 4. The three dimensional motion of the robot is shown in Figure 6.
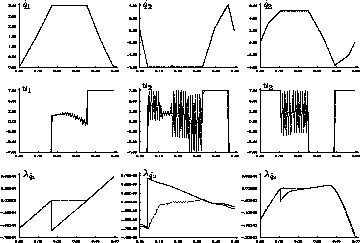
Figure 3: Solution curves for the state constrained time optimal
motion of the direct collocation method (--
--
--)
compared with the multiple shooting method (---
---
---).
In the curves of the angles 
there are no visible differences between the two solutions.
They
are shown in Figure 5.
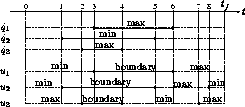
Figure 4: Switching structure of the state constrained time optimal motion.
Table 2: Estimated and final switching points of the state constrained time optimal motion.
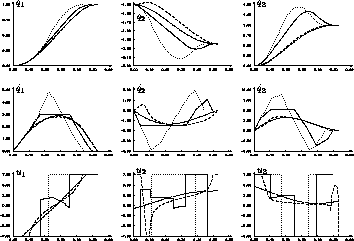
Figure 5: Solution curves of state and control variables for the
state constrained time optimal motion (---
---
---),
the minimum power consumption (-- -- --),
the minimum energy motion (--
--
--),
and the unconstrained time optimal motion (
).
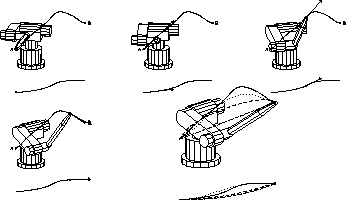
Figure 6: Five snapshots of the state constrained time optimal motion
from A (t=0) to B (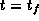
) at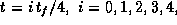 
and a comparison of the four trajectories.
Table 3: Comparison of results of the multiple shooting method for different objectives
(correct figures of the direct collocation method underlined,
denotes the optimum value, 
solution only computed by direct collocation).
Remark 4. The oscillating behaviour of the
discretized controls results from the
oscillating behaviour of the
only pointwise fulfilled state constraints on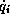 
.
This is a common behaviour of direct collocation
or direct shooting methods.
Also, when entering the constraint on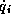 
the
control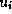 
is not continuous
and the
angular velocity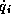 
is only
continuous but not differentiable at the
entry (and exit) point of the state constraint.
Therefore a better approximation of state and control
variables can be obtained
either by increasing the number of grid points
to a huge number
or by taking the switching structure
into account in a
so-called multi-stage or multi-phase
discretization, too ([26], [27]). I.e.,
the switching points
are introduced as additional variables
and the controls are allowed to be changed discontinuous
and the states to be changed not differentiable
at the switching points.
This adopted discretization
results in a more accurate solution of the direct collocation
method for the controls
and the objective value
with even less grid points
(cf. [26] for an example
and [27] for more details).
The non adopted standard discretization is
shown in Figure 3
to demonstrate the oscillating behaviour
on state constraint subarcs.
Remark 5. The adjoint variables and their estimates
seem to differ significantly on state constrained subarcs
(cf. Figure 3).
The estimates of adjoint variables obtained
by the direct collocation method
are related to the adjoint variables
from the necessary conditions of
Jacobson, Lele, and Speyer [12]
where the state constraints themselves
are coupled to the free Hamiltonian
with a multiplier function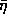 
For the formulation of the multi-point boundary value problem the necessary conditions of Bryson, Denham, and Dreyfus (Eq. (20)) have been used. Both sets of adjoint variables differ only along the state constrained subarcs and can be transformed into each other [17], [27].
When the state constrained minimum time motion
has been computed, solutions to the minimum power consumption and
the minimum energy criterion can be computed
to a prescribed final time that is
only about 10-15 % slower than the minimum time
and the constraints on the angular velocities
do not become active.
Here, we choose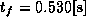 
that is
7 % slower than the minimum time.
The solution curves are shown in Figure 5
and compared with the minimum time solution.
To analyze the impact of the constraints on the angular velocities
on the time optimal motions,
the minimum time solution is computed where
the state constraints are not taken into account.
The resulting minimum time is
10 % faster than the state constrained minimum time
solution. But this solution violates the constraints
on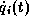 
, i=1,2,3, and on 
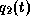and is shown in Figure 5.
Thus the constraints on the angular velocities play an important
role in the time optimal motion.
Remark 6. All solutions shown in Figure 5
have been obtained by the combination of the direct and the indirect method
besides the solution for the minimum power consumption criterion.
The only visible significant differences between the solutions of
both methods are in the state constrained time optimal motion
and are shown in Figure 3.
The differences in the objective values are listed in Table 3.
