


Next: Numerical Results
Up: Numerical Methods
Previous: Direct Collocation Method
Following [27] and [28] both methods
are combined as follows:
The direct collocation method is applied with
a poor initial guess of the solution 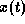 ,
, 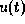 ,
i. e., with an initial trajectory that interpolates the
given values at initial and final time linearly.
The obtained (suboptimal) solution
provides reliable estimates of the state and adjoint
variables and of the switching structure
of state and control constraints
(cf. [26], [27]).
With this guess the multiple shooting method
is applied to the multi-point boundary value
problem resulting from the necessary conditions
of optimality.
For the derivation of the necessary conditions
we used the symbolic computation method
MAPLE [6]:
The equations of motion are explicitly given
in the appendix of [19]
in the form of Eq. (1).
First the explicit inverse of the mass matrix
,
i. e., with an initial trajectory that interpolates the
given values at initial and final time linearly.
The obtained (suboptimal) solution
provides reliable estimates of the state and adjoint
variables and of the switching structure
of state and control constraints
(cf. [26], [27]).
With this guess the multiple shooting method
is applied to the multi-point boundary value
problem resulting from the necessary conditions
of optimality.
For the derivation of the necessary conditions
we used the symbolic computation method
MAPLE [6]:
The equations of motion are explicitly given
in the appendix of [19]
in the form of Eq. (1).
First the explicit inverse of the mass matrix 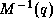 is computed.
Then the partial derivatives
of each component of the vector function
is computed.
Then the partial derivatives
of each component of the vector function
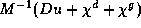 with respect to
with respect to 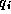 ,
, 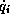 , i=1,2,3,
are derived.
As output of the MAPLE program
we obtain a FORTRAN code
for
, i=1,2,3,
are derived.
As output of the MAPLE program
we obtain a FORTRAN code
for 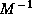 , the adjoint differential equations,
the Hamiltonian function
and the formulae for the boundary controls from
, the adjoint differential equations,
the Hamiltonian function
and the formulae for the boundary controls from
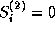 or
or 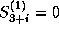 in the state constrained case.
The resulting FORTRAN codes
for the inverse mass matrix are about 630 lines and
for the adjoint differential equations
are about 3350 lines long although
in each step of the derivation
several optimization strategies
are applied in MAPLE to simplify the resulting formulae.
For more than three degrees of freedom it
might be more efficient to use
automatic differentiation [10]
and to make even more use of the
special structure of the robotic dynamics
in order to keep the number
of the resulting arithmetic operations as small as possible.
in the state constrained case.
The resulting FORTRAN codes
for the inverse mass matrix are about 630 lines and
for the adjoint differential equations
are about 3350 lines long although
in each step of the derivation
several optimization strategies
are applied in MAPLE to simplify the resulting formulae.
For more than three degrees of freedom it
might be more efficient to use
automatic differentiation [10]
and to make even more use of the
special structure of the robotic dynamics
in order to keep the number
of the resulting arithmetic operations as small as possible.
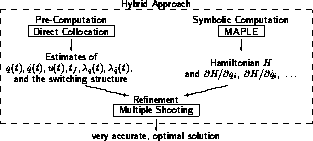
Figure 2: Combination of direct, indirect and symbolic methods in robot trajectory optimization.



Next: Numerical Results
Up: Numerical Methods
Previous: Direct Collocation Method
Oskar von Stryk
Fri Apr 5 21:57:02 MET DST 1996
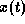 ,
, 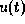 ,
i. e., with an initial trajectory that interpolates the
given values at initial and final time linearly.
The obtained (suboptimal) solution
provides reliable estimates of the state and adjoint
variables and of the switching structure
of state and control constraints
(cf. [26], [27]).
With this guess the multiple shooting method
is applied to the multi-point boundary value
problem resulting from the necessary conditions
of optimality.
For the derivation of the necessary conditions
we used the symbolic computation method
MAPLE [6]:
The equations of motion are explicitly given
in the appendix of [19]
in the form of Eq. (1).
First the explicit inverse of the mass matrix
,
i. e., with an initial trajectory that interpolates the
given values at initial and final time linearly.
The obtained (suboptimal) solution
provides reliable estimates of the state and adjoint
variables and of the switching structure
of state and control constraints
(cf. [26], [27]).
With this guess the multiple shooting method
is applied to the multi-point boundary value
problem resulting from the necessary conditions
of optimality.
For the derivation of the necessary conditions
we used the symbolic computation method
MAPLE [6]:
The equations of motion are explicitly given
in the appendix of [19]
in the form of Eq. (1).
First the explicit inverse of the mass matrix 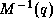 is computed.
Then the partial derivatives
of each component of the vector function
is computed.
Then the partial derivatives
of each component of the vector function
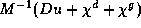 with respect to
with respect to 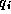 ,
, 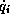 , i=1,2,3,
are derived.
As output of the MAPLE program
we obtain a FORTRAN code
for
, i=1,2,3,
are derived.
As output of the MAPLE program
we obtain a FORTRAN code
for 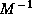 , the adjoint differential equations,
the Hamiltonian function
and the formulae for the boundary controls from
, the adjoint differential equations,
the Hamiltonian function
and the formulae for the boundary controls from
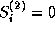 or
or 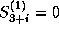 in the state constrained case.
The resulting FORTRAN codes
for the inverse mass matrix are about 630 lines and
for the adjoint differential equations
are about 3350 lines long although
in each step of the derivation
several optimization strategies
are applied in MAPLE to simplify the resulting formulae.
For more than three degrees of freedom it
might be more efficient to use
automatic differentiation [10]
and to make even more use of the
special structure of the robotic dynamics
in order to keep the number
of the resulting arithmetic operations as small as possible.
in the state constrained case.
The resulting FORTRAN codes
for the inverse mass matrix are about 630 lines and
for the adjoint differential equations
are about 3350 lines long although
in each step of the derivation
several optimization strategies
are applied in MAPLE to simplify the resulting formulae.
For more than three degrees of freedom it
might be more efficient to use
automatic differentiation [10]
and to make even more use of the
special structure of the robotic dynamics
in order to keep the number
of the resulting arithmetic operations as small as possible.
