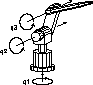
Figure 1: Three degrees of freedom in the DLR model 2 of the r3 robot.
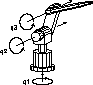
Figure 1: Three degrees of freedom in the DLR model 2 of the r3 robot.
We consider the Manutec r3 robot with 6 links. As the first 3 degrees of freedom (d.o.f.) are mainly responsible for the position and the last 3 d.o.f. for the orientation of the tool center point frame, we restrict ourself to the (first) 3 d.o.f. case. The DLR model 2 of the Manutec r3 robot was developed by Otter and Türk [19] and describes the motion of the links as a function of the control input signals of the robot drives
where 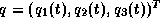 are the relative angles between
the arms,the normalized torque controls are
are the relative angles between
the arms,the normalized torque controls are
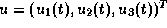 ,
,
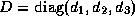 is a scaling matrix with
is a scaling matrix with  ,
,
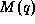 is the
positive definite and symmetric
is the
positive definite and symmetric 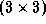 -matrix of moments
of inertia,
-matrix of moments
of inertia, 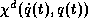 are the moments caused by
coriolis and centrifugal forces, and
are the moments caused by
coriolis and centrifugal forces, and 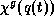 are the
moments caused by gravitational forces.
The final time
are the
moments caused by gravitational forces.
The final time 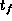 may be prescribed or free.
The full data of the dynamic model can be found in [19].
Just to give an impression of the model we give the structure
of the first element of the mass matrix M
may be prescribed or free.
The full data of the dynamic model can be found in [19].
Just to give an impression of the model we give the structure
of the first element of the mass matrix M
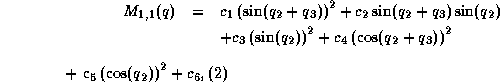
where 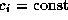 ,
, 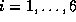 , and of the driving forces
, and of the driving forces 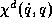
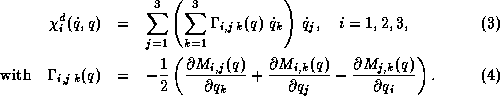
The dynamic behaviour of the robot
is now given either in an efficient implicit form of the right hand side
of 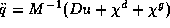 by the subroutine R3M2SI [19]
or explicitly by the output of a symbolic
computation system given in the appendix of [19].
by the subroutine R3M2SI [19]
or explicitly by the output of a symbolic
computation system given in the appendix of [19].
Point-to-point trajectories are to be considered, i. e.,
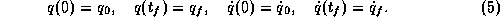
Here, we consider stationary boundary conditions, i. e.,
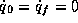 .
As objectives for optimal trajectories
three criterions are investigated:
The minimum time
.
As objectives for optimal trajectories
three criterions are investigated:
The minimum time
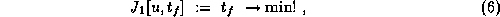
the minimum energy
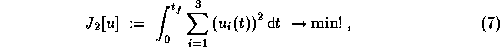
and the minimum power consumption (cf. [16], [21])
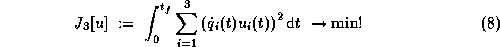
The final time 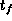 has to be prescribed for
has to be prescribed for 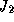 and
and 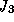 in
order to obtain useful solutions.
Otherwise, a free
in
order to obtain useful solutions.
Otherwise, a free 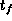 will tend to become very large.
Eighteen technical constraints
have to be considered (cf. [19]):
There are control constraints on the torque
voltages
will tend to become very large.
Eighteen technical constraints
have to be considered (cf. [19]):
There are control constraints on the torque
voltages
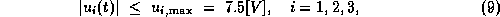
state constraints on the angles
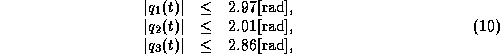
and state constraints on the angular velocities
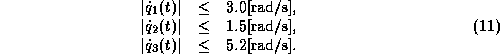
The numerical results show that the latter constraints become often active during the time optimal motions. Thus they play an important role within the optimization.