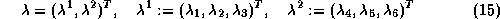
Necessary conditions of optimality are obtained via the minimum principle, cf., e. g., [3]. With the adjoint variables
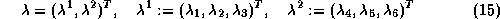
the Hamiltonian function of the unconstrained problem is
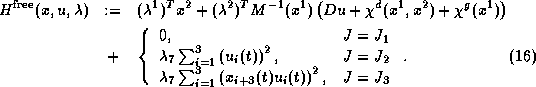
To have a uniform treatment of active upper or lower state constraints we introduce the new state constraints
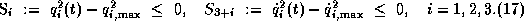
With the abbreviations for the total time derivatives of S
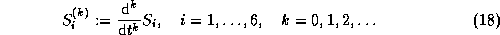
we find
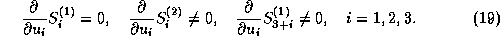
The functions 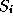 are second and the
are second and the 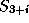 are first order state constraints.
Thus
the Hamiltonian becomes
(cf. Bryson, Denham, Dreyfus [2])
are first order state constraints.
Thus
the Hamiltonian becomes
(cf. Bryson, Denham, Dreyfus [2])
where 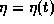 is a multiplier.
The necessary conditions from the minimum principle
yield for the state and adjoint variables
among others (cf. [20])
is a multiplier.
The necessary conditions from the minimum principle
yield for the state and adjoint variables
among others (cf. [20])
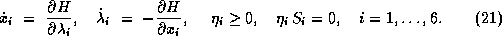
The optimal control is determined by the minimum principle
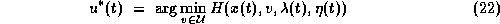
where 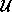 denotes the control space.
If
denotes the control space.
If 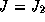 or
or 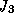 then
then 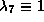 in
in 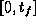 because
because
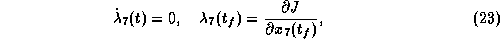
and  and
and  j=1,2,3, and the right hand sides of the first order
differential equations (13), (14)
do not depend on
j=1,2,3, and the right hand sides of the first order
differential equations (13), (14)
do not depend on  .
.
Furthermore,
it can be easily shown (for all three objectives) that 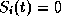 and
and 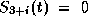 ,
i=1,2, or 3,
cannot occur at the same time
(cf. [20],
[22]).
,
i=1,2, or 3,
cannot occur at the same time
(cf. [20],
[22]).
In the time optimal motion (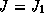 )
the controls appear linearly in H. Thus H is not regular.
If no state constraint is active the i-th optimal control
of bang-bang type
is determined by the sign of the switching function
)
the controls appear linearly in H. Thus H is not regular.
If no state constraint is active the i-th optimal control
of bang-bang type
is determined by the sign of the switching function 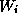
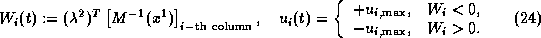
The case of a singular control, i. e., 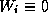 in a whole subinterval, did not occur
in the point-to-point trajectories considered here,
but might be possible, too.
in a whole subinterval, did not occur
in the point-to-point trajectories considered here,
but might be possible, too.
The minimum time 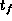 is determined by
is determined by
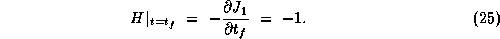
As 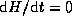 ,
, 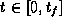 ,
it follows that
,
it follows that 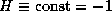 along the time optimal trajectory.
along the time optimal trajectory.
If the minimum power consumption (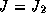 )
or the minimum energy criterion (
)
or the minimum energy criterion (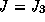 )
are chosen the unbounded optimal control
is determined by
)
are chosen the unbounded optimal control
is determined by
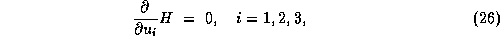
if 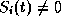 and
and 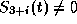 .
.
If 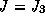 it can be shown
that if
it can be shown
that if 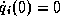 (i=1,2, or 3) then
there exists
(i=1,2, or 3) then
there exists 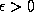 such that
such that
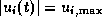 , for
, for 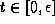 ,
and in the same way at
,
and in the same way at 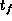 (cf. [20],
[22]).
(cf. [20],
[22]).
If a state constraint is active, e. g., 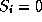 or
or
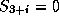 then
then 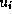 is determined from
is determined from
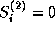 or
or 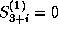 , resp., for any objective.
, resp., for any objective.
All in all, the necessary conditions can be
stated as a well-defined multi-point boundary value problem
if the optimal switching structure
of state and control constraints is known.
For more details we refer the interested reader
to [20].