The multiple shooting method
has shown to be an effective tool in solving
highly nonlinear multi-point boundary value problems.
The method is described, e. g., by Bulirsch [4]
and Stoer, Bulirsch [24].
Its application to a complicated state constrained optimal
control problem is described by
Bulirsch, Montrone, and Pesch [5].
Here, we used the code BNDSCO due to Oberle [18].
The main drawbacks when applying the multiple shooting
method in the numerical solution of optimal control problems are
1. the derivation of the necessary conditions
(e. g., the adjoint differential equations),
2. the estimation of the optimal switching structure,
and 3. the estimation of an appropriate initial
guess of the unknown
state and adjoint variables 
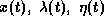in order to start the iteration process.
The great advantage of the multiple shooting method is
the verification of the optimality conditions
resulting in a highly accurate
solution.
To overcome the first drawback a good knowledge of optimal control
theory
is required. Proper estimates of the switching structure and of
the adjoint variables might then be provided by the use
of a homotopy or continuation technique.
This can be a very laborious task
(cf. [5] for an example)
that is especially cumbersome in our problem as none of the adjoint
variables is given either at 0 or 
.
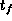In this paper we will demonstrate how the drawbacks 2 and 3
can be overcome when a direct collocation method
is used in a pre-computation to
estimate the optimal switching structure,
state and adjoint variables.
In the derivation of the necessary conditions
we used the symbolic computation method MAPLE due to
Char et al. [6].