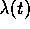 from the multipliers
of the discretized problem by
from the multipliers
of the discretized problem by
It has been shown in the previous section that the necessary conditions of optimality of the discretized problem reflect the necessary conditions of the original continuous problem. More precisely, it has been shown that Eq. (32) and Eq. (28), resp., are discretized versions of the adjoint differential equation (18) and the condition (19), respectively.
Therefore, we obtain an estimate of 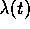 from the multipliers
of the discretized problem by
from the multipliers
of the discretized problem by
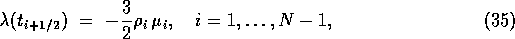
where 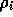 is a scaling factor depending on the discretization.
In addition, an estimate of
is a scaling factor depending on the discretization.
In addition, an estimate of 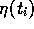 can be obtained from
can be obtained from 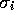 .
.
Another approach for estimating adjoint variables in combination
with a direct collocation method has been
used by Enright and Conway [8].
They used the multipliers 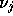 from Eq. (23)
of the boundary conditions
in the discretized problem
in order to estimate
from Eq. (23)
of the boundary conditions
in the discretized problem
in order to estimate 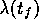 .
This estimate is then used as an initial value for the
backward integration of the
adjoint differential equations (18).
It is a well-known matter of fact that this backward integration
is crucial for highly nonlinear problems.
Also, state constraints were not considered.
.
This estimate is then used as an initial value for the
backward integration of the
adjoint differential equations (18).
It is a well-known matter of fact that this backward integration
is crucial for highly nonlinear problems.
Also, state constraints were not considered.
A further approach for estimating adjoint variables is based on an interpretation of the adjoint variables as sensitivities connected to the gradient of the cost function

where x satisfies the differential equations (2). This relation can be found, e. g., in Breakwell [2] or in Bryson, Ho [4]. In a discretized version as, e. g.,
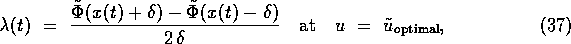
it can be used in combination with a direct shooting method
as, e. g., [1], with a suitable
steplength 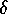 for the difference quotient.
Here, the superscript
for the difference quotient.
Here, the superscript  denotes that the variable or value has been
obtained numerically, e. g., by a direct shooting method.
For more details, cf., e. g., Eq. (29) in [1].
denotes that the variable or value has been
obtained numerically, e. g., by a direct shooting method.
For more details, cf., e. g., Eq. (29) in [1].
The guess of adjoint variables by direct methods is usually
affected by several sources of inaccuracies and troubles.
First, the
suboptimal control  calculated by a direct method
is often inaccurate
and can differ significantly from the optimal control.
Second, the accuracy of the calculated objective
calculated by a direct method
is often inaccurate
and can differ significantly from the optimal control.
Second, the accuracy of the calculated objective
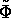 is often not better than one percent.
In addition, the case of nearly active or inactive state variable inequality
constraints has not yet been included in a reliable manner in previous attempts.
is often not better than one percent.
In addition, the case of nearly active or inactive state variable inequality
constraints has not yet been included in a reliable manner in previous attempts.
In contrast to the former approaches, the quality of the estimated adjoints does neither depend crucially on a highly accurate computation of the cost function or the calculated suboptimal control nor the appearance of active state constraints following our approach. As it is shown from the examples and the reported numerical results in this paper and in [6], [17], and [18], the new way of estimating adjoint variables herein proposed is very reliable and accurate even for complicated and highly nonlinear problems and problems including state constraints. Furthermore, convergence properties of the discretization scheme have been derived.