 -vector function of adjoint or costate variables
-vector function of adjoint or costate variables 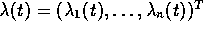 and a multiplier function
and a multiplier function 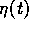 .
With the Hamiltonian
.
With the Hamiltonian
There exist an  -vector function of adjoint or costate variables
-vector function of adjoint or costate variables 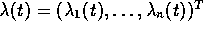 and a multiplier function
and a multiplier function 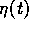 .
With the Hamiltonian
.
With the Hamiltonian
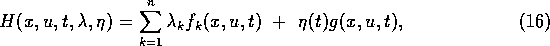
the necessary first order conditions of optimality result in a multi-point boundary value problem
The original boundary constraints (3) and
additional
constraints on 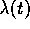 at
at 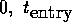 ,
, 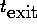 , and
, and 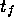 also have to
be fulfilled.
In general, at junction points
also have to
be fulfilled.
In general, at junction points  ,
, 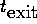 ,
the adjoint variables may have discontinuities.
For more details cf. Bryson, Ho [4] and Hestenes [12] and also
Jacobson, Lele, Speyer [13],
Maurer [15],
and the results of
Maurer cited in Bulirsch, Montrone, Pesch [5]
for the necessary conditions of optimality in the constrained case.
,
the adjoint variables may have discontinuities.
For more details cf. Bryson, Ho [4] and Hestenes [12] and also
Jacobson, Lele, Speyer [13],
Maurer [15],
and the results of
Maurer cited in Bulirsch, Montrone, Pesch [5]
for the necessary conditions of optimality in the constrained case.
In the sequel, we shall see that the necessary first order optimality
conditions of the
continuous problem are reflected
in the necessary first order optimality conditions of the discretized problem.