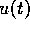 and the final time
and the final time 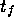 that minimize the functional
that minimize the functional
Systems governed by ordinary differential equations arise in many applications as, e. g., in astronautics, aeronautics, robotics, and economics. The task of optimizing these systems leads to the optimal control problems investigated in this paper.
The aim is to find a control vector 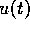 and the final time
and the final time 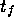 that minimize the functional
that minimize the functional

subject to a system of  nonlinear differential equations
nonlinear differential equations
boundary conditions
and 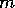 inequality constraints
inequality constraints
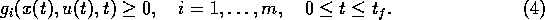
Here, the 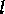 vector of control variables is denoted by
vector of control variables is denoted by 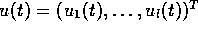 and the
and the  vector of state variables is denoted by
vector of state variables is denoted by 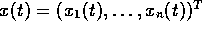 .
The functions
.
The functions 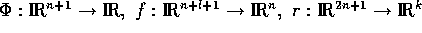 , and
, and 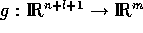 are assumed to be continuously differentiable.
The controls
are assumed to be continuously differentiable.
The controls 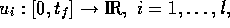 are assumed to be bounded and measureable and
are assumed to be bounded and measureable and 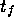 may be fixed or free.
may be fixed or free.