Minimum Time and Minimum Energy Trajectories of an Industrial Robot
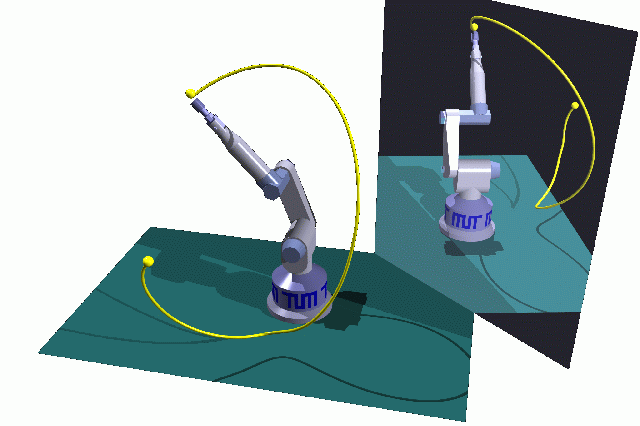
Summary
Minimum time and minimum energy point-to-point trajectories
for an industrial robot of type Manutec r3 have been computed
subject to a full nonlinear dynamical model of the
robot dynamics taking into account forces and moments
resulting from inertia, coriolis, centrifugal and gravitational effects.
Furthermore, states on the control variables
as well as on the state variables
(as upper and lower bounds on the angular velocities and others)
have been considered.
The developed optimization method DIRCOLhas demonstrated
remarkable robustness and efficiency.
The numerical results also show that the constraints
on the angular velocities become active during large parts
of the minimum time trajectory.
But the resulting stress on the links can be significantly reduced
by a minimum energy trajectory that is only about fifteen percent
slower than the minimum time trajectory.
The optimization problem and the numerical solution approach
have originally been presented in Chapter 8.4 of the doctoral dissertation.
The animation has been implemented by Alexander Heim
using the interactive graphics system SIGMA.
Videos
Problemstellung:
Intro.avi (12fps/1.961 KB)
Intro.avi (24fps/3.405 KB)
Intro.mpg (2.507 KB)
Zeitminimale
Lösung:
Zeit.avi (12fps/2.201 KB)
Zeit.avi (24fps/3.504 KB)
Zeit.mpg (4.026 KB)
Energieminimale
Lösung:
Energ.avi (12fps/2.427 KB)
Energ.avi (24fps/3.859 KB)
Energ.mpg (4.157 KB)
Vergleich der beiden Bahnen:
Vergl.avi (12fps/3.146 KB)
Vergl.avi (24fps,5.236 KB)
Vergl.mpg (5.057 KB)
Relevant Publications
-
Heim, A.; von Stryk, O.:
Trajectory optimization of industrial robots with application to computer-aided robotics and robot controllers.
Optimization 47 (2000) 407-420.
PostScript file (16160kb),
gzipped PostScript file (375kb),
PDF file (8068kb),
gzipped PDF file (287kb).
-
M. Glocker, M. Vögel, O. von Stryk:
Trajectory optimization of a shuttle mounted robot.
In: Proc. Workshop on Optimal Control in Hypersonic Flight,
Greifswald, 7.-8. Oktober 1999 (München: Hieronymus Verlag, 2000) 71-82.
-
Heim, A.; von Stryk, O.; Pesch, H.J.; Schäffler, H.; Scheuer, K.:
Parameteridentifikation, Bahnoptimierung und Echtzeitsteuerung
von Robotern in der industriellen Anwendung.
In: Hoffmann, Jäger, Lohmann, Schunck (eds.):
Mathematik - Schlüsseltechnologie für die Zukunft
(Springer Verlag, 1997) 551-564.
PostScript file (11722kb),
gzipped PostScript file (452kb),
PDF file (552kb).
-
von Stryk, O.:
Numerische Lösung optimaler Steuerungsprobleme:
Diskretisierung, Parameteroptimierung und Berechnung der
adjungierten Variablen.
Dissertation (München: Technische Universität,
Mathematisches Institut, 1994).
Fortschritt-Berichte VDI, Reihe 8, Nr. 441, VDI-Verlag,
Düsseldorf, 158 S., 1995.
-
von Stryk, O.; Schlemmer, M.:
Optimal control of the industrial robot Manutec r3.
In: R. Bulirsch, D. Kraft (Hrsg.): Computational Optimal Control, International Series of Numerical Mathematics 115 (Basel: Birkhäuser, 1994) 367-382.
Preprint: Schwerpunktprogramm der Deutschen Forschungsgemeinschaft: Anwendungsbezogene Optimierung und Steuerung, Report No. 467, Mathematisches Institut, Technische Universität München (1993).
PostScript file (507kb),
gzipped PostScript file (110kb).
-
von Stryk, O.; Pesch, H.J.; Bulirsch, R.:
Zeit ist Geld? Nicht für Roboter!
Sonderreihe: Forschung für Bayern, Heft Nr. 6 (Technische Universität München, 1993) 22-23.
(please click here for gif files of pages
22,
23)
Fachgebiet Simulation und Systemoptimierung, TU Darmstadt
