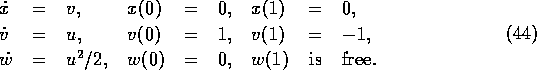
This well-known problem is due to Bryson, Denham, and Dreyfus [3]. After a transformation, the differential equations and boundary conditions are
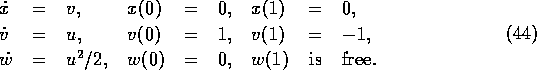
The objective is
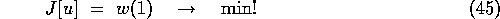
The state constraint to be taken into account is of order 2 here
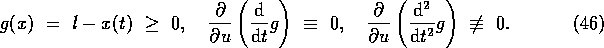
Explicit formulae of the solution depending on the value of l
can be given, cf. [3], [4].
For 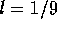 , there exists an interior boundary arc
, there exists an interior boundary arc
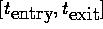 =
=
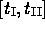 =
= 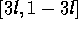 where the state constraint is
active.
The minimum objective value is
where the state constraint is
active.
The minimum objective value is 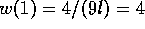 .
With the Hamiltonian
.
With the Hamiltonian
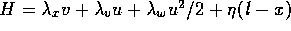 the minimum principle yields for the adjoint variables
the minimum principle yields for the adjoint variables
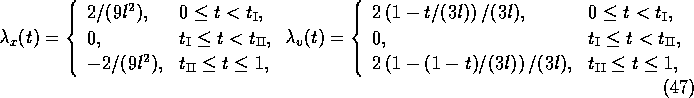
and 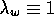 .
The adjoint variable
.
The adjoint variable 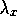 suffers discontinuities
when entering or leaving the state constraint.
A first solution is obtained by using DIRCOL with an equidistant grid
of N=11 grid points resulting in a minimum objective value of
suffers discontinuities
when entering or leaving the state constraint.
A first solution is obtained by using DIRCOL with an equidistant grid
of N=11 grid points resulting in a minimum objective value of 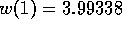 .
In Figs. 7 to 10 these first suboptimal solutions are shown by dashed lines
and the exact solutions are shown by solid lines.
In addition, the grid points of the discretization are marked.
.
In Figs. 7 to 10 these first suboptimal solutions are shown by dashed lines
and the exact solutions are shown by solid lines.
In addition, the grid points of the discretization are marked.
*[-1.6cm]
=5.2cm =7.3cm ZZZG67_x.epsf
=5.2cm =7.3cm ZZZG67_a.epsf
*[0.3cm]
Fig. 7: The state variable x.
Fig. 8: The control variable u.

*[-3.0cm]
=5.2cm =7.3cm ZZZG67_lambda_x.epsf
=5.2cm =7.3cm ZZZG67_lambda_v.epsf
*[0.3cm]
Fig. 9: The adjoint variable 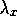 .
Fig. 10: The adjoint variable
.
Fig. 10: The adjoint variable 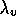 .
.
The solution is now refined by using a ``three-stage'' collocation approach
that includes the switching structure of the state constraint, i. e.
the switching points 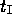 and
and 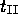 are included as
two additional parameters
with two additional equality conditions in the
optimization procedure
are included as
two additional parameters
with two additional equality conditions in the
optimization procedure
*[-0.3cm]
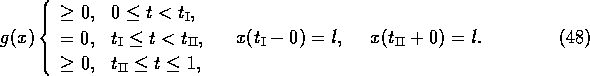
The method DIRCOL is now applied to the reformulated problem with a separate grid of 4 grid points
in each of the three stages 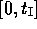 ,
, 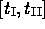 ,
and
,
and 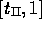 . This results in a minimum objective value of
. This results in a minimum objective value of 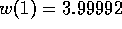 and a more accurately satisfied state constraint.
In Figs. 11 to 14 the refined solutions are shown. In addition,
two dotted vertical lines show
the entry and exit points
of the state constraint that are computed with an error of one percent.
The quality of the estimated adjoint variables and also of the control variable
has been significantly improved while the dimension of the resulting
nonlinear program has not been increased.
and a more accurately satisfied state constraint.
In Figs. 11 to 14 the refined solutions are shown. In addition,
two dotted vertical lines show
the entry and exit points
of the state constraint that are computed with an error of one percent.
The quality of the estimated adjoint variables and also of the control variable
has been significantly improved while the dimension of the resulting
nonlinear program has not been increased.
*[-1.6cm]
=5.2cm =7.3cm ZZZG67_x3.epsf
=5.2cm =7.3cm ZZZG67_a3.epsf
*[0.3cm]
Fig. 11: The state variable x.
Fig. 12: The control variable u.
*[-1.6cm]
=5.2cm =7.3cm ZZZG67_lambda_x3.epsf
=5.2cm =7.3cm ZZZG67_lambda_v3.epsf
*[0.3cm]
Fig. 13: The adjoint variable 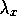 .
Fig. 14: The adjoint variable
.
Fig. 14: The adjoint variable 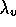 .
.