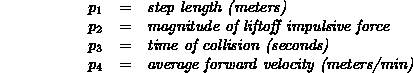
As we are solving a finite-time problem, the boundary constraints of the biped walking problem represent an important part of the problem definition. We allow a number of parameters to be variable. These are as follows:
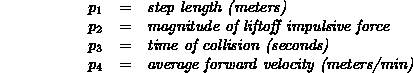
At the initial and final time, periodicity of the states and controls
must be enforced while in between phases continuity is enforced.
Another boundary constraint is that
if an impulsive liftoff force is included at the beginning of phase 1,
then the velocities must reflect the sudden jump caused
by the impulsive force.
Given the magnitude of the impulsive force 
,
the Collision Algorithm can
determine the resulting new velocities for the beginning of phase 1.
A further boundary constraint is
the swing leg must also land at the time of collision, 
, at a step
size equal to 
.
Since in our experiments we constrain the proportion of phase 1 to 85%
of the total time of the walking step,
the final or total time (also variable)
may be determined from the phase 1 duration .