Appendix: Reduced Dynamics Algorithm

 

With the introduction of holonomic constraints, such as the contact of legs with the ground, it is possible to construct a set of reduced unconstrained dynamics of dimension equal to the number of degrees of freedom, N, minus the number of constraints, m. In this section, we outline our approach to calculating the independent generalized accelerations of the reduced set of dynamics. The novelty of this approach is that it does not require the explicit construction of the reduced dynamics. It will be shown how one may extract the solution of the reduced dynamics from the solution of the Contact Algorithm and the solution of the forward dynamics of the entire system. One main advantage of using a reduced unconstrained dynamical model is that optimization programs which require integration of the dynamics will encounter less numerical difficulties.

In order to satisfy the constraint condition (), the generalized velocities must belong to the null space of the constraint Jacobian, . If the columns of X represents a basis for , then there exists a representation of with respect to X denoted here by , . Substituting into the dynamical equations and multiplying on the left by will give us the reduced dynamics,

 

where , , , and .

If represents the generalized coordinates of the system, then it is possible to choose N-m independent coordinates and m dependent coordinates such that may be used as an alternative expression for (). This approach was made in [12], and it leads to an obvious choice for X,

 

An advantage of making this choice for the basis X is that, as will be shown in the Reduced Dynamics Algorithm, the reduced accelerations are simply represented as . Our goal here is to show that the solution of the contact algorithm may be used to obtain a solution of the reduced forward dynamics problem. Then an optimization routine performing numerical integration need only integrate on the independent coordinates . We first give a lemma before the algorithm is presented.

 

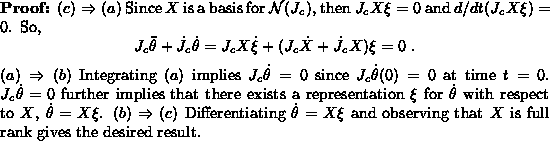
Reduced Dynamics Algorithm

1. Beginning with an independent set of coordinates , solve via inverse kinematics for from . Similarly solve for from using the algebraic relation .
2. Given a set of torque inputs u, one may solve for with the contact algorithm. Simple algebraic manipulation shows that this solution satisfies (a) of Lemma .
3. Using Equation (), it follows that , and it satisfies the reduced dynamics ().

This algorithm thus yields the reduced forward dynamics mapping .