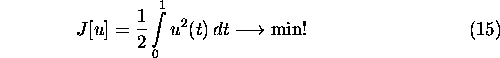
This well-known problem is reported in Sec.3.11, Example 2, of Bryson, Ho [5]. The task is to minimize
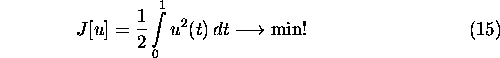
subject to the differential equations and boundary conditions
![]()
and subject to the state variable inequality constraint
![]()
First the objective has to be transformed into Mayer type by introducing a third state variable
![]()
Then the objective to be minimized is
![]()
Now the dynamic model has the dimensions
NY = DIMY = 3, NV = DIMV = 0, NU = DIMU = 1, NP = NPAR = 0, NRB = NRB = 5, NZB = NZB = 1.
A formula of the solution can be given explicitly (see [5]
for details).
For l;SPMgt;1/4 the inequality constraint does not become active,
for ![]() the inequality constraint becomes active
at a touch point at t=0.5, and
for
the inequality constraint becomes active
at a touch point at t=0.5, and
for ![]() the inequality constraint becomes active
a along a whole subarc of [0,1].
the inequality constraint becomes active
a along a whole subarc of [0,1].
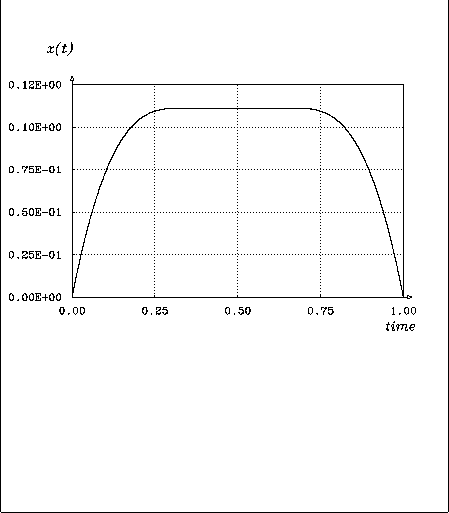
Figure: Optimal x(t) for an upper bound of ![]()
The unconstrained problem (NZB = 0) can be investigated first. Next, the state constrained problem can be investigated by setting NZB = 1 and l properly (for example, l=1/6 or 1/9). The behaviour of the solution may now be studied for a sequence of increased or decreased values of l.