A proper scaling of all dependent and independent variables and functions may effect the efficiency and robustness of any numerical algorithm used on computers with limited arithmetic precision.
It is therefore recommendable to scale
the state variables y(t) and v(t),
the control variables u(t)
and also the objective function ![]() properly
by applying suitable linear transformations.
properly
by applying suitable linear transformations.
As a rule of thumb, the range of the transformed variables
![]() ,
, ![]() and
and ![]() should be approximately [-1,+1] (after scaling).
If the original range of the variables is not known a priori
one may get a first idea by looking at the initial trajectories.
should be approximately [-1,+1] (after scaling).
If the original range of the variables is not known a priori
one may get a first idea by looking at the initial trajectories.
For the purpose of scaling by linear transformation the formulas
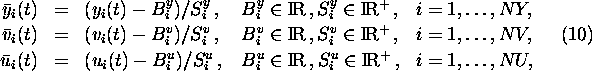
are used. The constants
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() have to be selected properly in order to transform the ranges
of the state variables
and the control variables onto [-1,+1] (as a rule of thumb).
have to be selected properly in order to transform the ranges
of the state variables
and the control variables onto [-1,+1] (as a rule of thumb).
In the same manner, the objective can be transformed by
![]()
As a rule of thumb, the minimum value of the transformed objective
should be approximately 1000 and the range of variation
of the transformed objective ![]() should be between zero and 1000.
should be between zero and 1000.
The scalings by linear transformations are optionally. The constants defining the linear transformations can be provided in this section using the syntax
variable = value of
As variable one may use
The linear transformations are then applied internally.
The user does not have to deal with the transformed variables.
Input, output and problem dependent subroutines are handled
in the original units of all variables and functions.
Example:
Looking at the initial trajectory of an optimal control problem from flight mechanics
one may find that that the differential state variable
These constants for the internal linear transformation of
in section SKALIERUNG of the input file.
![]() value of factor
value of factor ![]()

![]() (altitude) does have a range of approximately
(altitude) does have a range of approximately
![]() (meters) to
(meters) to ![]() (meters).
In this case, it may be useful to select
(meters).
In this case, it may be useful to select
![]() and
and ![]() .
.
![]() are now supplied to the program by the line
Y( 1) = 240.0E+3 210.0E+3
are now supplied to the program by the line
Y( 1) = 240.0E+3 210.0E+3