


Next: Parameter estimation problems
Up: PurposeProblem Descriptions, and
Previous: Abstract
The dynamic model is described by a system of differential-algebraic
equations of index 1 in semi-explicit form:
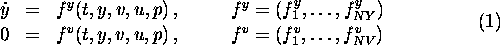
Notation
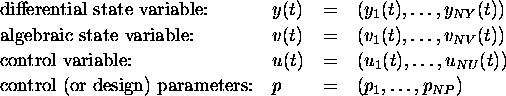
(In the case of a dynamical system of only ordinary differential equations
NV is zero.)
Further problem dependent functions are:
- boundary conditions (including initial and final conditions
of the state variables) defined by
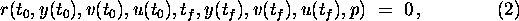
where 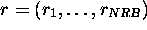 ,
,
- (nonlinear) inequality constraints
on the control and state variables
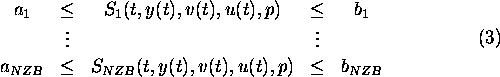
(Constraints of this kind usually appear more often in optimal control
than in parameter estimation problems.)
- (general) functions of the state (and control) variables
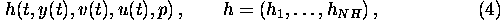
which may be used for two different purposes:
- In parameter identification problems
the state variables y(t) and v(t) often
cannot be measured directly. But functions h of them
have been measured in an experiment.
The relation between the measured quantities
and the state variables is given by the function
h(t,y,v,u,p).
- PGRAPH also generates graphical output of the functions
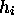 . Therefore any functions
. Therefore any functions 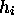 of the state and
control variables might be used in addition for
the purpose of monitoring properties of the
computed trajectories
(for example, phase diagrams as the altitude/velocity
diagram in optimal control problems from flight mechanics,
or violations of algebraic index-2- or index-3-constraints
if index reduction has been applied to a problem
with a system of differential-algebraic equations
of a higher index (as in the pendulum problem
described in Section 5.1)).
of the state and
control variables might be used in addition for
the purpose of monitoring properties of the
computed trajectories
(for example, phase diagrams as the altitude/velocity
diagram in optimal control problems from flight mechanics,
or violations of algebraic index-2- or index-3-constraints
if index reduction has been applied to a problem
with a system of differential-algebraic equations
of a higher index (as in the pendulum problem
described in Section 5.1)).
The components of the functions 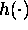 do only enter
the optimization program PAREST if they are required
in a parameter estimation problem.
Otherwise they will only be used for plotting by PGRAPH.
do only enter
the optimization program PAREST if they are required
in a parameter estimation problem.
Otherwise they will only be used for plotting by PGRAPH.
Oskar von Stryk
Tue Feb 1 13:50:42 CET 2000
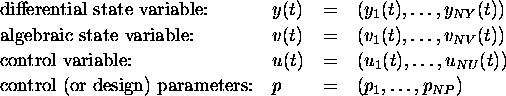
![]() ,
,![]() do only enter
the optimization program PAREST if they are required
in a parameter estimation problem.
Otherwise they will only be used for plotting by PGRAPH.
do only enter
the optimization program PAREST if they are required
in a parameter estimation problem.
Otherwise they will only be used for plotting by PGRAPH.